I. Cartografía mental del texto:
II. Resumen:
El
proceso de enseñanza de la matemática debe realizarse de tal manera que los
estudiantes incorporen nuevos conocimientos y desarrollen habilidades que les
permitan aplicar estos mismos de tal forma que así sean capaces de resolver
problemas de su entorno social.
Sin
embargo esto pocas veces se cumple, pues se presentan en los contenidos
matemáticos (aritméticos y geométricos), deficiencias especialmente los
relacionados a la geometría como por ejemplo el reconocimiento de propiedades
de las figuras y cuerpos geométricos.
Según
Proenza Garrido y Leyva (2008), para que se desarrolle el pensamiento
geométrico es necesaria la tarea del docente a la hora de impartir estos
contenidos, ya que el docente se debe agenciar de diversas formas a la hora de
enseñar la geometría empleando modelos didácticos que le sirvan de apoyo para
que el estudiante desarrolle su pensamiento geométrico.
En
síntesis se debe propiciar al momento de enseñar la geometría que los
estudiantes se enfrenten a situaciones que requieran de sus conocimientos,
habilidades y capacidades geométricas.
III. Problema y características:
Se
constata que en el nivel primario de educación escolar, algunos docentes
enseñan contenidos de geometría de forma convencional.
ü Algunos
profesores sólo se encargan de transmitir contenidos sobre geometría, sin
propiciar situaciones vivenciales en los que los niños los puedan poner en
práctica.
ü Los
estudiantes se enfrentan muy pocas veces a situaciones que requieren de sus
conocimientos, habilidades y capacidades geométricas.
ü En
la enseñanza de la geometría pocos docentes tienen la idea equivocada que el
conocimiento geométrico presupone solamente el reconocer visualmente una
determinada forma y saber el nombre correcto.
ü Poca
utilización de modelos didácticos al enseñar contenidos geométricos.
ü Se
emplea muchas veces solo una manera para enseñar la geometría.
IV. Fundamentación:
1. Aprendizaje de la matemática:
ü La
enseñanza de la matemática ha de realizarse de un modo donde los estudiantes se
apropien de los conocimientos y desarrollen habilidades que les permitan aplicar sus conocimientos para resolver los problemas
del entorno social.
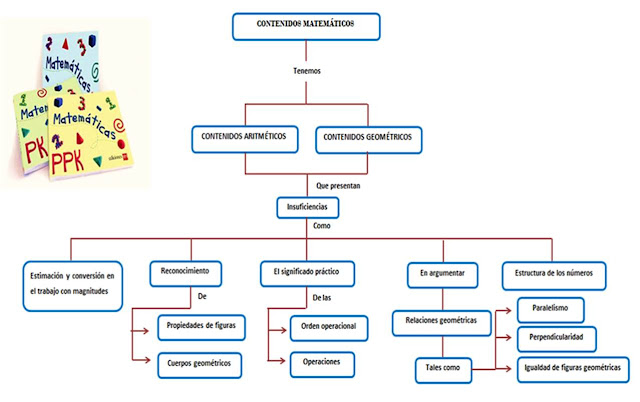
ü Los contenidos matemáticos son los aritméticos y geométricos.
ü En el proceso de E-A de los contenidos matemáticos se presentan
insuficiencias tales como el orden en la estructura de los números; la
estimación y conversión en el trabajo con magnitudes; el significado práctico
de las operaciones y orden operacional;
el reconocimiento de propiedades de figuras y cuerpos geométricos y en
argumentar utilizando relaciones geométricas: paralelismo, perpendicularidad, igualdad
de figuras geométricas.
2. Contenidos geométricos:
ü Su
enseñanza se centra en el trabajo exhaustivo de elementos de geometría
espacial.
ü Se
desarrollan en los programas de nociones elementales incluyendo tres
componentes como círculos infantiles, vías no formales y grado preescolar.
ü Estos
contenidos al igual que la matemática influyen en el desarrollo del pensamiento
lógico en los escolares de nivel primario.
ü Para
enseñar estos contenidos es necesaria la aplicación de modelos didácticos como
por ejemplo el modelo de los niveles de razonamiento de Van Hiele.
3. Pensamiento matemático:
ü Según
los autores este tipo de pensamiento debe ser más flexible, creativo,
divergente y verdadero.
ü Según
Schoenfeld utilizar este pensamiento significa desarrollar un punto de vista
matemático valorando el proceso de matematización y abstracción.
ü Según
Proenza G.y Leyva L. (2008) este pensamiento es aquel que se potencia a través
de conocimientos, habilidades y capacidades matemáticas que sirven para
resolver problemas de la vida.
4. Pensamiento geométrico:
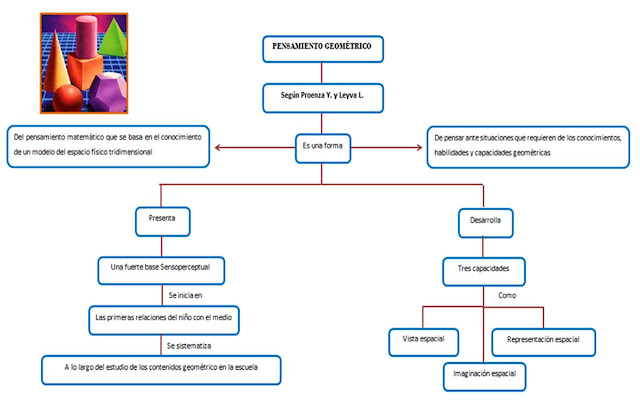
ü Según
Proenza G.y Leyva L. (2008) el pensamiento geométrico es una forma de
matemático, además es una manera de pensar ante situaciones que requieren de
los conocimientos, habilidades y capacidades geométricas.
ü El
pensamiento geométrico debe desarrollar tres capacidades como vista espacial,
representación espacial e imaginación espacial.
ü Engloba
el conocimiento geométrico que implica explorar el espacio, comparar elementos
observados, establecer relaciones entre ellos, descubrir propiedades de las
figuras, construir modelos, elaborar conclusiones, formular leyes y resolver
problemas.
ü El
pensamiento geométrico presenta tres niveles que son matematización, donde se
requiere de la percepción sensorial directa de objetos; reconocimiento, se
establece relaciones y elaboración donde ante situaciones el estudiante
resuelve problemas
V. Juicio crítico:
Actualmente
se observa que al momento de enseñar las matemáticas en la escuela primaria los
profesores, se basan en formas establecidas, es decir en un conjunto de
operaciones y fórmulas que ya están dadas y que el estudiante debe
aprendérselas para poder desarrollar sus operaciones, sin muchas veces
comprender lo que hacen. Así de esta manera terminan olvidándose lo que han
aprendido, encontrando complicada las matemáticas.
Es
este problema que manifiestan los autores, principalmente en la enseñanza de la
geometría que es lamentable. Porque muchas los profesores están acostumbrados a
enseñar solo de una misma manera la geometría, sin saber que se debe tener
mucho cuidado al momento de enseñar esta área, ya que si se impartieran bien su aprendizaje a través del empleo de
modelos didácticos se estaría potenciando el desarrollo del pensamiento
geométrico en el estudiante.
Para
que de esta forma el niño sea capaz de construir su propio esquema mental del
espacio, incorporando en el progresivamente, todas las nociones sobre
geometría.
En síntesis
concuerdo con la propuesta y visión del autor ya que refleja la triste realidad
que se presenta en las escuelas, al momento de enseñar las matemáticas
especialmente los contenidos geométricos, donde es ahí que los niños mecanizan
y no comprenden
Entonces
me parecería como un llamado de atención después de leer este documento, para
poder reflexionar y no cometer estos errores, tratar de enseñar la matemática
propiciando el descubrimiento por parte del estudiante que es el elemento
fundamental en el proceso de enseñanza y aprendizaje.
VI. Conclusiones:
1.
Determinar
el nivel de desarrollo del pensamiento matemático, es un problema que debe ser
resuelto por sus sistemas educativos.
2.
La
enseñanza de la matemática con los niños debe trabajarse en diferentes maneras
ya sea una de ellas es el transmitir conocimientos para resolver situaciones
prácticas.
3.
Sabiendo
que el verdadero aprendizaje de la geometría comienza en la escuela, los
profesores deben ayudar a sus niños a concienciar sus experiencias y poner en marcha su pensamiento geométrico.
4.
El
estudiante del nivel primario debe ser capaz de construir el propio esquema
mental del espacio, incorporando en el progresivamente, todas las nociones
sobre geometría.
5.
Los
niveles del pensamiento geométrico son tres el primero es matematización,
reconocimiento y elaboración.
6.
El
pensamiento geométrico es una forma de pensar ante situaciones que requieren de
los conocimientos, habilidades y capacidades geométricas.
VII. Referencias:
[En línea] http://funes.uniandes.edu.
[Consulta: 30 de marzo del 2013]
VIII. Anexos:




No hay comentarios:
Publicar un comentario